Mongoose

Теория тяготения Эйнштейна и особенности понимания библейской тверди святым Григорием Нисским

Прежде чем перейти к изложению взглядов святого Григория Нисского, рассмотрим представления науки о пространстве, его форме.

Развитие геометрии: от Евклида до Римана

Евклидова геометрия

В III веке до Р.Х. в Александрии появилось сочинение Евклида «Начала», в котором геометрия излагалась в систематическом виде. В основу построения Евклида положен ряд первоначальных утверждений (постулатов), которые не доказываются. Все остальные утверждения (теоремы) выводятся из постулатов логически. Всего Евклидом сформулировано пять постулатов геометрии. Но особое внимание продолжателей и комментаторов Евклида было приковано к постулату о пересекающихся прямых: «Когда прямая, пересекая две прямые, образует внутренние односторонние углы, составляющие в сумме меньше двух прямых углов, эти прямые при продолжении пересекаются в точке, лежащей с той стороны, где расположены эти углы»[1].

Отсутствие непосредственной очевидности постулата, сложность его формулировки (в сравнении с лаконичностью и наглядностью других постулатов Евклида) неоднократно в истории науки вызывали предположение, что постулат о параллельных возможно доказать. Но окончательный ответ на вопрос о возможности доказательства постулата был дан русским ученым Н.И. Лобачевским.

Геометрия Лобачевского

В своей работе «О началах геометрии» (1829) Лобачевский заявил, что допущение постулата, противоположного постулату Евклида, позволяет построить другую геометрию, отличную от Евклидовой и свободную от внутренних противоречий.

Что именно Лобачевский счел возможным изменить в евклидовой геометрии? Лобачевский принял все аксиомы Евклида, кроме аксиомы параллельных, которую он заменил следующей аксиомой: пусть в данной плоскости дана прямая и лежащая вне этой прямой точка; тогда через эту точку можно провести к данной прямой в данной плоскости две различные параллельные прямые[2]. Эта аксиома, а также четыре остальных аксиомы Евклида, истинность которых Лобачевский не подвергал сомнению, заложили основу для построения новой геометрии.

Геометрия Лобачевского многими не была принята. В качестве главного аргумента звучало обвинение в отсутствии наглядности. Новая геометрия казалась первым в истории науки абстрактным математическим объектом. Но настолько же абстрактной является и евклидова геометрия, что справедливо отмечал Лобачевский: «В природе нет ни прямых, ни кривых линий, нет плоскостей и кривых поверхностей, в ней находим одни тела, так что все прочее создано нашим воображением, существует только в теории»[3].

В попытке доказать непротиворечивость собственной геометрии Лобачевский опирался на пример сферической геометрии, в истинности которой сомнений ни у кого не существовало. Эта геометрия известна со времен эллинистической древности. Степень ее развития уже тогда мало отличалась от степени развития евклидовой геометрии. Начало сферической геометрии положил, по-видимому, еще Евдокс (IV в. До Р.Х.), а систематическое изложение этой науки принадлежит Менелаю Александрийскому[4]. Сферическая геометрия реализовывалась на обычной сфере в евклидовом пространстве, поэтому она и не вызывала у математиков чувства протеста.

Лобачевский установил, что соотношения между сторонами и углами треугольников сферической геометрии при определенном допущении (замена действительного радиуса сферы мнимым (комплексным) числом) совпадают с соответствующими формулами его геометрии. Из этого он заключал, что, если бы формулы его геометрии содержали в себе противоречие, то такое же противоречие содержала бы и сферическая геометрия. Но поскольку истинность сферической геометрии не подвергалась сомнению, то следовало признать и непротиворечивость конкретных формул геометрии Лобачевского. Важным следствием новой геометрии, которая называется гиперболической, является тот факт, что сумма углов треугольника в геометрии Лобачевского всегда меньше π[5]. Недостаток этой суммы до числа π называется дефектом треугольника (разница между суммой углов сферического треугольника и числом π называется избытком треугольника). Дефект треугольника непосредственно связан с другой величиной – радиусом кривизны пространства Лобачевского. Радиус кривизны участвует во всех формулах гиперболической геометрии Лобачевского. Важный вывод, который следует из формул Лобачевского, гласит, что при бесконечно большом радиусе кривизны угол параллельности равен π/2, то есть выполняются законы евклидовой геометрии. Другими словами, Лобачевский считал, что евклидова геометрия является частным случаем его геометрии. В этом и заключается преимущество, универсальность геометрии Лобачевского: она ни в коем случае не отменяет законов евклидовой геометрии, но включает их в свои построения как предельный случай.

Лобачевский настаивал на том, что аксиомы должны иметь опытное происхождение: «Первые понятия, с которых начинается какая-нибудь наука, должны быть ясны и приведены к самому меньшему числу. Тогда только они могут служить прочным и достаточным основанием учения. Такие понятия приобретаются чувствами, врожденным – не должно верить».

В качестве опытной проверки истинности своей геометрии Лобачевский считал возможными задействовать только астрономические наблюдения. Эта необходимость была продиктована все теми же формулами Лобачевского: различия для треугольников евклидовой и гиперболической геометрии выявляются тем сильнее, чем больше площадь самого треугольника. Лобачевский был первым, кто поставил вопрос о возможной искривленности пространства в космологических масштабах.

Отсутствие внутренних противоречий в гиперболической тригонометрии еще само по себе не снимало вопрос о непротиворечивости геометрии Лобачевского в целом. Вопрос был бы полностью решен, если бы удалось найти такие объекты в евклидовом пространстве, на которых реализовывалась бы вся геометрия Лобачевского в целом.

Лобачевский ставил вопрос об опытной проверке теории параллельных. Вот что он писал по этому поводу: «Напрасные старания со времен Евклида, в продолжение двух тысяч лет, заставили меня подозревать, что в самих понятиях еще не заключается той истины, которую хотели доказывать и которую проверить могут лишь опыты, каковы, например, астрономические наблюдения».

Почему Лобачевский переходит к астрономическим наблюдениям? Он пытался установить экспериментально, какая геометрия имеет место в реальном мире – евклидова или «воображаемая», как он сам называл свою геометрию. Основываясь на данных астрономических наблюдений, Лобачевский пытался найти ответ на этот вопрос. Вывод его был таким: «В треугольнике, которого бока равняются почти с расстоянием Земли до Солнца, сумма углов не может разниться с двумя прямыми более 0,0003 секунды градуса».

Геометрия кривых поверхностей Гаусса

В построении новой, неевклидовой, геометрии Лобачевский был не одинок. Из опубликованной переписки одного из крупнейших математиков Карла Фридриха Гаусса (1777–1855) стало известно, что Гаусс вывел первые формулы новой геометрии задолго до Лобачевского. Однако дальше разработки самых элементарных теорем Гаусс не пошел и о результатах своих исследований никогда не высказывался, не желая стать объектом критики. Однако Гаусс хорошо известен как основной разработчик теории поверхностей. Его работа «Общее исследование кривых поверхностей», опубликованная в 1827 году, сыграла важную роль в развитии этой теории.

Идея нового подхода к теории поверхностей зародилась у Гаусса в 1820 году, когда ему было поручено произвести геодезическую съемку земли Ганновер. Специфической особенностью геодезии является необходимость проведения измерений на поверхности Земли, то есть на искривленной поверхности. Гаусс впервые обратил внимание на выделение в самостоятельный класс тех свойств поверхности, которые могут быть обнаружены путем измерений, проводимых на самой поверхности, без обращения к окружающему эту поверхность пространству. Совокупность этих метрических свойств называют внутренней геометрией поверхности. К числу компонентов метрической формы поверхности относятся расстояние между двумя точками, угол между пересекающимися линиями, площадь фигуры на поверхности. Гаусс установил, что, если две поверхности имеют одинаковые метрические формы, то их внутренние геометрии совпадают. Например, если на плоском листе бумаги начертить треугольник, то при изгибании листа бумаги (без растяжения или сжатия поверхности листа) мы получим изогнутый треугольник, но обладающий теми же метрическими параметрами, что и плоский: длина стороны, величина углов, площадь треугольника. В таком случае говорится, что исходная поверхность и поверхность, образованная изгибанием, обладают одинаковой внутренней геометрией.

Гаусс сумел решить вопрос о кривизне поверхности. Он установил, что кривизна поверхности может быть вычислена через метрическую форму. Эта величина – кривизна поверхности – получила название гауссовой кривизны. На любой поверхности можно строить геометрию точно так же, как на поверхности сферы. Роль прямолинейных отрезков играют геодезические линии, являющиеся кратчайшими линиями, соединяющими две точки поверхности. С помощью геодезических линий на поверхности строится геодезический треугольник. В зависимости от структуры поверхности гауссова кривизна для разных точек треугольника может иметь разное значение. Кроме того, она может принимать как положительное, так и отрицательное значение, в зависимости от того, имеет треугольник избыток или недостаток. Гауссова кривизна может быть постоянной (например, для сферы) или иметь различное значение (для произвольных искривленных поверхностей).

Сферическая геометрия, известная с древних времен, трактуется в построениях Гаусса как геометрия поверхности постоянной положительной кривизны. Геометрия Лобачевского – как геометрия поверхностей постоянной отрицательной кривизны. Евклидова геометрия рассматривается как геометрия поверхности постоянной нулевой кривизны.

Главное значение работ Гаусса заключается в установлении взаимосвязи между кривизной поверхности и ее метрическими формами. Было установлено, что кривизну поверхности можно вычислять, оставаясь на ней, не обращаясь к окружающему ее пространству.

Результаты Гаусса подвигли его ученика Бернгарда Римана к решению проблемы, как измерить кривизну пространства.

Формирование римановой геометрии

Основываясь на достижениях Гаусса, Бернгард Риман попытался ответить на вопрос, что же такое кривизна пространства и как она измеряется. Для определения кривизны в конкретной точке Риман применил тот же способ, каким Гаусс измерял кривизну поверхности, – подсчитывал сумму углов треугольника, составленного из отрезков геодезических линий, и смотрел, насколько она отличается от числа π. Но в пространстве через точку можно провести много плоскостей, и кривизна зависит не только от того, в какой точке ее вычисляют, но и от того, в какой плоскости лежат треугольники. Поэтому Риман говорит о кривизне в данной точке в направлении данной плоскости.

Если для всех треугольников в пространстве сумма углов равна π, то в этом пространстве верна обычная геометрия Евклида. Такое пространство не имеет кривизны, оно «плоское». Если есть треугольник, сумма углов которого больше π, то кривизна пространства в направлении плоскости этого треугольника в соответствующих точках положительна, если сумма меньше π, то отрицательна.

Обобщая гауссову теорию поверхностей на многомерный случай, Риман впервые ввел понятие тензор кривизны. Впоследствии этот элемент геометрии Римана вошел в уравнения Эйнштейна.

Выше было отмечено, что гауссова кривизна определяется только метрикой поверхности. Поверхности постоянной кривизны отличаются тем, что фигуры при перемещении на таких поверхностях сохраняют свои метрические формы – изгибание фигуры, как это имеет место при перемещении треугольника на псевдосфере, на метрические формы не влияет. Обобщая эту особенность на пространство, Риман сделал вывод, что в пространствах постоянной кривизны объекты при перемещении также сохраняют свои метрические формы, не меняются в размерах. Переменная же кривизна пространства должна приводить к деформации объекта при перемещении[6].

Риман, также как и Лобачевский, и Гаусс, поставил вопрос, является ли пространство, в котором мы живем, искривленным. В 1854 году в стенах Геттингенского университета Риман прочитал доклад «О гипотезах, лежащих в основании геометрии». С этого доклада начинается риманова геометрия. Важным вкладом в развитие римановой геометрии было создание итальянским геометром Г. Риччи-Курбастро и его учеником Леви-Чивита на рубеже XX века тензорного исчисления. В 1900 году они опубликовали одну из самых известных работ по теории тензорного исчисления – «Methodes de calcul differential absolu et leures applications», которую А. Эйнштейн использовал как математическую основу общей теории относительности.

Теория тяготения: от Ньютона к Эйнштейну

Революционную модель «геометрии» Вселенной предложил Альберт Эйнштейн, который в рамках развития общей теории относительности (далее ОТО) пришел к пониманию искривления пространства-времени в пределах гравитационного поля. В дорелятивистской ньютоновской физике господствовала модель бесконечной Вселенной с евклидовой геометрией. Эйнштейн пришел к представлению о конечной по объему, но не имеющей границ Вселенной с неевклидовой метрикой пространства. В основе разработки новой космологической модели лежало совмещение нескольких физических открытий конца XIX – начала XX века, к рассмотрению которых необходимо перейти.

Интерпретация классического принципа относительности А. Эйнштейном

Выше (см. часть 2 настоящей работы) была рассмотрена история возникновения и становления специальной теории относительности (СТО). Главный физический смысл этой теории, как уже было отмечено, заключается в том, что физические законы в разных инерциальных системах отсчета (ИСО) остаются инвариантными относительно преобразований Лоренца. (В классической механике все физические законы были инвариантны относительно преобразований Галилея). Важно то, что преобразования Лоренца при скоростях ИСО, значительно уступающих скорости света (движение объектов в макромире), фактически (в пределах погрешности измерений) выглядят как преобразования Галилея. Таким образом, преобразования Галилея являются частным случаем преобразований Лоренца. Но ни сам Лоренц, ни Пуанкаре, который дал правильную математическую формулировку преобразований, не отказывались от теории эфира. Последнее означало, что теоретически можно говорить об абсолютно покоящейся ИСО, неподверженной сокращениям, по отношению к которой все остальные ИСО испытывают сокращения и, следовательно, нуждаются в преобразованиях для того, чтобы классический принцип относительности охватывал все существующие ИСО и физические законы в них оставались бы инвариантными относительно указанных преобразований.

Но только Эйнштейн первым понял, что не имеет смысла привлекать понятие эфира для того, чтобы доказывать принцип относительности. Эйнштейн поставил вопрос по-иному. Классический принцип относительности Галилея он взял за аксиому. Отказ от эфира, наличие которого не подтверждалось опытным путем, означал, что абсолютно неподвижной ИСО не существует вовсе, ибо за неимением эфира пропадает ориентир для установления таковой. В таком случае и покоящаяся (уже в относительном, по ньютоновскому употреблению термина, пространстве), и движущаяся системы координат равноправны. Поэтому эффект сокращения времени и линейных размеров может быть наблюдаем не только из «покоящейся» системы относительно движущейся, но в равной степени и в обратном направлении: наблюдатель в движущейся системе будет наблюдать лоренцево сокращение в покоящейся системе.

Согласно специальному принципу относительности, «нет никакой особо предпочитаемой системы координат, которая давала бы повод к принятию идеи эфира, а вместе с тем нет никакого эфирного ветра, нет и экспериментов, долженствующих его обнаружить. Сокращение движущихся тел вытекает здесь из обоих основных начал теории без всяких особых гипотез. (Здесь под началами теории Эйнштейн подразумевает принцип относительности Галилея и постоянство скорости света в вакууме. – и.А.). При этом для сокращения тел определяющим является не какое-то движение в себе, во что мы не могли бы вложить никакого смысла, а движение по отношению к определенному, для данного случая избираемому исходному телу»[7].

Предположение сокращений Лоренца Эйнштейн принял, и оно стало важным звеном в цепочке дальнейших умозаключений Эйнштейна.

Принцип эквивалентности масс

Другое важное открытие в создании Эйнштейном теории тяготения вытекает из принципа эквивалентности гравитационной и инерционной масс. Понятия инерционной и гравитационной масс различались еще в классической механике Ньютона. В современной физике под этими массами понимают два различных свойства физического объекта. Инерционная масса характеризует меру инертности тела. Инерционная масса фигурирует во втором законе Ньютона. Гравитационная масса показывает, с какой силой тело взаимодействует с внешними гравитационными полями (пассивная гравитационная масса) и какое гравитационное поле создает само это тело (активная гравитационная масса). Гравитационная масса фигурирует в законе всемирного тяготения. Принцип равенства этих двух масс был выдвинут самим Ньютоном, а само равенство было установлено им экспериментальным путем с относительной точностью 10^-3. В конце XIX века более точные эксперименты провел Лоранд фон Этвеш, доведя точность до 10^-9. Равенство инерционной и гравитационной масс составляет содержание слабого принципа эквивалентности. Этот принцип стал важным элементом при формировании Альбертом Эйнштейном общего принципа относительности.

Слабый принцип эквивалентности масс позволил прийти Эйнштейну к очень важному умозаключению. Он предположил, что два явления – инерция и гравитация, – столь различные в формулировке Ньютона, должны иметь общее происхождение[8]. В качестве демонстрации этого предположения Эйнштейн предлагает провести следующий воображаемый эксперимент. Представим себе обширную часть пустого мирового пространства. Представим себе в качестве исходного тела просторный ящик в виде комнаты. Внутри находится наблюдатель. Для него не существует никакой тяжести. В середине крышки ящика с наружной стороны вмонтирован крюк с привязанным к нему канатом. И вот некоторое существо, безразлично какое, начинает тащить за этот канат с постоянной силой. Тогда ящик вместе с наблюдателем начинает лететь «вверх» в равномерно ускоренном полете. С течением времени его скорость возрастает до фантастических размеров, если судить об этом с другого исходного тела. Как представляется все событие человеку в ящике? Ускорение ящика переносится на него путем давления от пола ящика. Поэтому он должен принять это давление, упираясь ногами в пол. В своем ящике он тогда стоит совершенно так же, как любой из нас в комнате какого-либо дома на земле. Если он выпускает из рук какой-нибудь предмет, то на последний уже не передается ускорение ящика, и предмет поэтому будет приближаться к полу ящика в равномерно ускоренном относительном движении. Тогда наблюдатель придет к выводу, что он вместе со своим ящиком находится в некотором неизменном во времени поле тяготения. Обнаружив крюк в середине крышки ящика, наблюдатель последовательно заключит, что ящик подвешен в поле тяготения и потому находится в состоянии покоя. На внутренней стороне крышки ящика наш наблюдатель укрепляет веревку и к свободному ее концу подвязывает какой-либо предмет. Подвязанный предмет заставит веревку повиснуть «вертикально» в натянутом состоянии. Где причина этого натянутого состояния веревки? Человек в ящике решит, что на подвешенное тело действует в поле тяготения сила, влекущая его вниз и уравновешиваемая напряжением веревки, а величину напряжения веревки определяет гравитационная масса подвешенного тела. Напротив, наблюдатель, свободно парящий в пространстве, рассудит так: «Ускоренное движение ящика увлекает за собой веревку, которая тянет за собой в этом движении подвешенный к ней предмет. Напряжение веревки должно быть как раз настолько велико, чтобы могло вызвать ускоренное движение предмета. Величину напряжения веревки определяет инертная масса тела».

Классическая механика различает инерциальное движение тела и движение тела под действием гравитационного поля. Но согласно слабому принципу эквивалентности масс, это различие теряет силу, ибо, переходя к некоторой ускоренной системе отсчета, мы можем трактовать равномерное прямолинейное движение, обусловленное инерцией, как криволинейное ускоренное движение, которое уже невозможно отличить от движения, обусловленного гравитационным полем. По этому поводу Макс Борн замечает: «Фактически эффект гравитации никак невозможно отличить от эффекта ускорения; оба они полностью эквивалентны друг другу»[9].

В мысленном эксперименте с ящиком Эйнштейн расширил применение принципа относительности классической механики на тела, имеющие ускорение по отношению друг к другу. Тем самым он обобщил постулат относительности до всех систем отсчета, как инерциальных, так и движущихся с ускорением либо с вращением. Этот новый принцип относительности именуется общим принципом относительности.

Кривизна пространства в теории А. Эйнштейна

Эйнштейн предлагает, установив некоторую общность гравитации и ускорения, теоретическим путем установить свойства поля тяготения. Эйнштейн приводит мысленный эксперимент с вращающимся диском и двумя наблюдателями, проводящими независимые друг от друга измерения на диске. Этот эксперимент обнаруживает нарушение законов евклидовой геометрии в гравитационном поле (на основании соединения положений теории Лоренца и общего принципа относительности) В нижеприведенном мысленном эксперименте Эйнштейн попытался дать физическое истолкование пространственных данных с учетом общего принципа относительности.

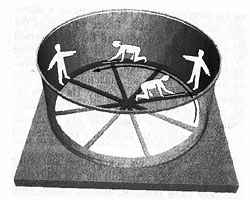
Итак, дан вращающийся диск с находящимся на нем наблюдателем. Пусть диск вращается равномерно. Наблюдатель № 1, эксцентрически сидящий на диске, почувствует силу, влекущую его по радиусу в противоположном от центра направлении. Наблюдатель № 2, находящийся вне вращающегося диска в состоянии покоя (в ИСО), объяснит эту силу как действие инерции (центробежную силу). Но наблюдатель № 1 может рассматривать свой диск также как покоящееся тело, а все остальные системы, в том числе и систему наблюдателя № 2, – как вращающиеся вокруг оси диска. Право на это ему дает общий принцип относительности. В таком случае наблюдатель № 1 будет воспринимать силу, действующую на него, как действие поля тяготения со стороны обода диска. Дальше оба наблюдателя начинают экспериментировать с мерами длины. Предполагается измерение длины окружности вращающегося диска. На результаты опыта начинает влиять лоренцево сокращение. Выглядит это следующим образом. Если наблюдатель № 1 свою меру длины (линейку), принятую за единицу, положит по периферии вращающегося диска, то для наблюдателя № 2 эта мера, оцениваемая из состояния покоя, будет короче единицы, потому что движущиеся тела сокращаются в направлении своего движения. Важно, что оба наблюдателя измеряют длину окружности заведомо вращающегося диска, каждый из своей системы (состояние покоящегося диска не рассматривается). В итоге измерения покоящегося наблюдателя № 2 при помощи своего эталона длины приводят к результату длины вращающейся окружности ℓ, а измерения наблюдателя на диске № 1 своим эталоном длины, подверженным лоренцеву сокращению, дают результат длины вращающейся окружности ℓ¹. При этом ℓ¹>ℓ. (Это происходит потому, что вследствие сокращения длины линейки наблюдателю № 1 придется прикладывать свою линейку большее число раз, чтобы обмерить всю окружность). Если же линейка будет положена по радиусу диска, то она, с точки зрения обоих наблюдателей, не испытает никакого сокращения (радиус как линейный размер будет перпендикулярен по отношению к вектору движения, и лоренцево сокращение на него передаваться не будет). В итоге при одинаковом для обоих наблюдателей радиусе длина окружности в измерениях наблюдателя № 1 будет больше, чем результат наблюдателя № 2. Для покоящегося наблюдателя выполняется значение числа π, равное π=ℓ/2r . В то время как для наблюдателя на вращающемся диске вследствие неравенства ℓ¹>ℓ число π будет иметь другое – большее – значение. Таким образом, «положения евклидовой геометрии не могут в точности выполняться на вращающемся диске и вообще в пределах поля тяготения, по крайней мере постольку, поскольку одной и той же мере придают всюду и во всех направлениях значение единицы длины. С тем вместе и понятие прямой линии теряет свое значение. Мы поэтому не в состоянии дать точное определение координатам x, y, z в отношении к диску по установленному в специальной теории относительности методу»[10].

Сокращение масштабов длины и времени в пределах гравитационного поля стало революционным заявлением в физике. В частности, Макс Борн называет его крушением представлений о евклидовой пространственно-временной Вселенной, так как привычные понятия – прямая линия, плоскость, круг – по причине изменения масштабов перестают соответствовать действительности[11]. Суть новых пространственно-временных характеристик Эйнштейн иллюстрирует предположением о криволинейной траектории светового луча в пределах полей тяготения: «По отношению к Галилееву исходному телу К (здесь тело К совершает равномерное и прямолинейное движение. – и.А.) луч света распространяется по прямой линии со скоростью с. Но в отношении к находящемуся в состоянии ускоренного движения ящику (здесь Эйнштейн имеет ввиду ящик, эксперимент с которым был рассмотрен выше. – и.А.) путь того же самого луча, как это легко вывести, уже не будет прямолинеен. Отсюда следует заключить, что лучи света в пределах полей тяготения распространяются по кривой линии»[12].

Нарушение привычных законов геометрии в пределах полей тяготения заставили Эйнштейна обратиться к неевклидовым геометрическим моделям. Эйнштейн вводит понятие неевклидова континуума. Если на обычной евклидовой плоскости построить ортогональную систему координат, то положение любой точки плоскости можно определить с помощью двух чисел относительно любой другой точки. Эти два числа есть не что иное, как декартовы координаты. Совокупность точек, геометрическое место которых задается декартовыми координатами, образует евклидов континуум. Эйнштейн предлагает деформировать евклидову плоскость. В таком случае применима только гауссова система координат. Геометрическое место точек в этой системе определяется пересекающимися кривыми линиями. Расстояние между точками такой поверхности определяется по специальному уравнению. Этот метод, разработанный самим Гауссом, применялся им, как известно, при геодезических измерениях (на кривых поверхностях – континуум двух измерений). Но метод также может быть применим и к континууму большего числа измерений. Это обобщение гауссова метода осуществил, как рассматривалось выше, Риман. Эйнштейн же воспользовался готовыми разработками геометрии Гаусса с обобщениями Римана.

Ввиду искажений, которым подвергаются координаты и время в пределах полей тяготения, Эйнштейн пришел к выводу, что пространственно-временной континуум не может более восприниматься как евклидов. В таком континууме теряет всякий смысл понятие о евклидовой прямой.

Недостаток теории гравитации Ньютона заключается в том, что механизм гравитации никак не объясняется. В ньютоновской теории тяготения Солнце удерживает Землю и другие планеты на некоторой «привязи». Это воздействие передается мгновенно на любое расстояние, но сама природа воздействия не определена. Эйнштейн предложил новую концепцию гравитации. Пространство, лишенное материи, является «плоским». Присутствие массы «искривляет» пространство (уже знакомая риманова кривизна пространства). Идея Эйнштейна заключается в том, что в пределах поля тяготения все тела движутся по экстремальным (геодезическим) линиям. В частности, Земля вращается вокруг Солнца по кратчайшей (геодезической) траектории, возможной в искривленном Солнцем пространстве – по окружности[13].

Таким образом, главным достижением Эйнштейна является то, что он указал механизм, с помощью которого действует гравитация. Этим механизмом является кривизна пространства. Кривизна пространства и есть само тяготение. (В механике Ньютона таким механизмом была абстрактная «привязь», в то время как структура пространства не претерпевала никаких изменений в связи с присутствием в нем гравитационных масс).

Сферический мир Эйнштейна

Эйнштейн охарактеризовал нашу искривленную Вселенную как трехмерную сферу[14].

Кроме того, эта Вселенная характеризуется конечностью объема и отсутствием краев[15]. Понимание трехмерной сферы Эйнштейна, конечной по объему, но не имеющей «краев», доступно, опять же, с помощью заключений по аналогии. Вернемся к разумному двумерному существу, которое живет уже не просто на искривленной поверхности, а на замкнутой искривленной поверхности. Предельно наглядным примером служит двумерная сфера, погруженная в обычное трехмерное пространство. Поскольку для существа доступны только две координаты на такой поверхности, отбросим наши представления о радиусе сферы, ее диаметре и вообще всякой хорде. (Впрочем, географические координаты на поверхности Земли задаются, как известно, именно двумя координатами: географической широтой и долготой.) Допустим, что кривизна такой поверхности стремится к нулю (а значит, согласно Гауссу, радиус такой поверхности стремится к бесконечности), а существо очень маленькое. На небольших площадях оно, проводя измерения, не обнаружит отклонений от законов евклидовой геометрии, по крайней мере, в пределах погрешности самих измерений. По этой причине существо будет говорить о не имеющем пределов евклидовом пространстве своей «вселенной». Но, потратив достаточное время и передвигаясь по «прямой» (которая на самом деле является геодезической линией кривых поверхностей; на поверхности сферы это дуга большого круга), существо вернется в исходную точку, но с «другой» стороны. Таким образом, оно заключит о конечном объеме своей Вселенной, но в то же время и об отсутствии «краев», каких-либо границ, ставящих предел его передвижению. Трехмерная сфера Эйнштейна обладает свойствами, аналогичными свойствам рассмотренной двумерной сферы. Только в трехмерной сфере не имеет «краев» уже не поверхность сферы, а ее объем. Проецируя полученный результат на трехмерную сферу Эйнштейна, обладающую конечным объемом и не имеющую границ, можно заключить и о бесконечности передвижения в конечном объеме в любом направлении.

Следует отметить, что в начальном варианте сферическая Вселенная Эйнштейна была стационарна, неизменна во времени. В уравнения Эйнштейна, связывающие между собой свойства материи, заполняющей искривленное пространство-время, с его кривизной, входит так называемая космологическая постоянная – физическая постоянная, характеризующая свойства вакуума[16]. Но советский ученый Александр Фридман в 1922 году показал, что введение космологической постоянной не есть необходимость. В данной работе космологические модели не рассматриваются, но стоит добавить, что позже Эйнштейн признал свою ошибку и согласился с нестационарной моделью Вселенной Фридмана.

Экспериментальная проверка общей теории относительности (ОТО)